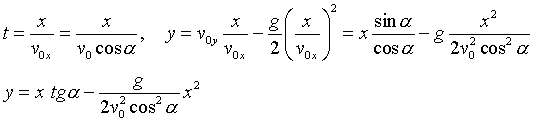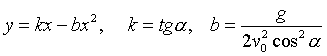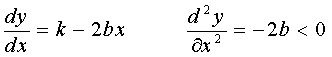Назад

Движение тела, брошенного под углом к горизонту.

 

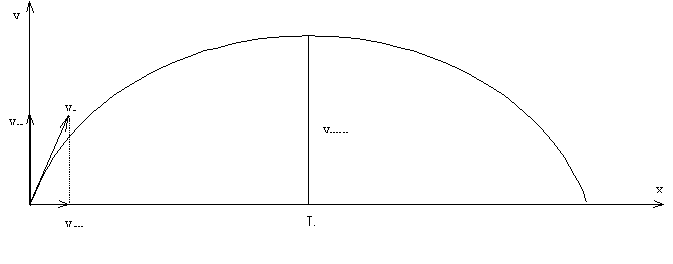
В качестве сложного движения рассмотрим движение точечной массы брошенной под углом  a к горизонту со скоростью v₀.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

В этом случае точка одновременно движется равномерно со скоростью v_ox вдоль оси Х и равнозамедленно с начальной скоростью  v_y  вдоль оси У. ( а = g )

Уравнение движения точки имеют вид:

          x = v_0xt,                                            где   v_0x = v₀ cos α

         

          y = v_0yt – gt²/2,                                 где   v_0y = v₀ sin α

 

Для нахождения уравнения траектории движения необходимо из системы  уравнений исключить время:

Полученное выражение представляет собой уравнение параболы:

            

Для нахождения y_max  необходимо найти первую производную указанной функции по Х и приравнять ее к нулю, определить вторую произ­водную и исследовать ее знак. Если вторая производная меньше 0, то функция действительно имеет максимум.

                

Следовательно,   у = y_max      при   x=k/2b    т.е.

 

Все записанное справедливо, если отсутствует или достаточно мало сопротивление среды, в которой движется материальная точка. Таким образом, наибольшая дальность полета в отсутствии сил сопротивления наблюдается при движении тела под углом в 45° к горизонту.