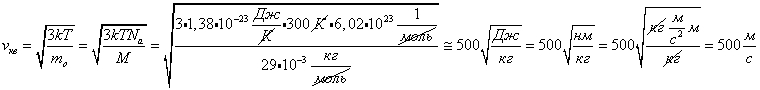К оглавлению раздела На главную

Расчёт скорости движения молекул.

Введение. Температура, как мера средней кинетической энергии молекул

Попробуем получить нетривиальные результаты, используя уравнение Клайперона-Менделеева и основное уравнение МКТ.

Введем понятие средней кинетической энергии молекул:

(1)

Преобразуем основное уравнение МКТ с учетом формулы (1):

т.е. основное уравнение МКТ запишем так (2)

Воспользуемся уравнением К.-М. в таком виде:

(3)

Сравним уравнения (2) и (3) и получим, что

или (4)

Как понимать формулу (4)?

Мы выяснили, что от температуры зависит величина средней кинетической энергии молекул. Поэтому говорят, что температура - мера средней кинетической энергии молекул. Это утверждение мы доказали на для идеального газа, но оказывается оно справедливо и для других агрегатных сосятояний вещества.

Среднеквадратичная скорость движения молекул.

Интересен вопрос о скорости движения молекул газа. В газен царит полный хаос, молекулы движутся по всем направлениям с самыми разными скоростями.

Оказывается, что

1. в газе есть молекулы с очень маленькими скоростями и с очень большими, но их сравнительно мало.
2. Средняя проекция скорости на любое направление для всего газа равна 0 (иначе, в газе существовали бы потоки).
3. Оказывается у молекул есть средняя скорость (по модулю), которая зависит от температуры, и основная часть молекул имеет модуль скорости близкий к ней. Эту скорость мы не можем вычислить, но можем легко посчитать среднеквадратичную скорость движения молекул газа, которая отличается от средней скорости коэффициентом порядка 1.

Определение. Среднеквадратичная скорость молекул равна квадратному корню из среднего квадрата скорости молекул:

(5)

Вычислим среднеквадратичную скорость из средней кинетической энергии молекул, которую мы легко можем сосчитать:

(6)

С учетом уравнения (4) получим:

(7)

Посчитаем, например, среднюю скорость молекул газа в классной комнате:

T=300K, m_o=M/N_a, М=0,029 г/моль. С учетом этого имеем: